原题链接

Rudolf and Subway

1. 做完后记得选择这个选择题。 {{ select(1) }}

• 提交并且通过了
• 还没有提交，或者提交了 WA 了。

题目描述

建桥对伯纳德没有帮助，他去哪里都迟到。然后鲁道夫决定教他乘坐地铁。

鲁道夫将地铁地图描绘成一个无向连接图，没有自循环，其中顶点代表车站。任何一对顶点之间最多有一条边。

如果可以绕过其他站点，则可以通过一条边直接在相应站点之间移动，则两个顶点通过一条边连接。鲁道夫和伯纳德居住的城市的地铁有颜色符号。这意味着站点之间的任何边缘都具有特定的颜色。特定颜色的边缘共同形成一条地铁线。地铁线不能包含未连接的边，并形成给定地铁图的连接子图。

地铁地图示例如图所示。

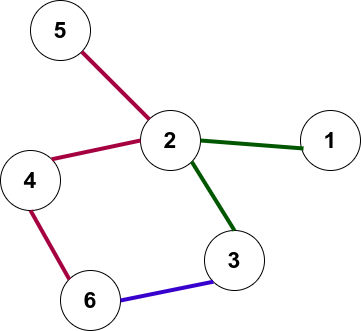
鲁道夫声称，如果这条路线通过最少数量的地铁线路，这条路线将是最佳的。

帮助 Bernard 确定给定出发站和目的地站的最小数量。

输入格式

第一行包含一个整数 $t$ ( $1 \le t \le 10^4$ ) 表示测试用例的数量。

接下来是测试用例的描述。

每个测试用例的第一行包含两个整数 $n$ and $m$ ( $ 2 \le n \le 2 \cdot 10^5, 1 \le m \le 2 \cdot 10^5 $ ) 表示地铁站数量和车站之间的直达路线数量 (即图形边缘).

紧随其后的是 $m$ 行 表示边缘的描述。描述的每一行包含三个整数 $u$ , $v$ , and $c$ ( $ 1 \le u, v \le n, u \ne v, 1 \le c \le 2 \cdot 10^5 $ ) ） — 有一条边的顶点的数目，以及这条边的颜色。保证相同颜色的边形成给定地铁图的连接子图。任意两个顶点的一对之间最多有一条边。

后面跟着两个整数 $b$ 和 $e$ ( $1 \le b, e \le n$ ) 表示出发站和目的地站。

所有测试用例上所有 $n$ 的总和不超过 $2 \cdot 10^5$ . 所有的总和 $m$ 在所有测试用例中不超过 $2 \cdot 10^5$ .

输出格式

对于每个测试用例，输出一个整数 — 从车站 $b$ 到车站 $e$ 的路线可以通过的最小地铁线路数。

5
6 6
1 2 1
2 3 1
5 2 2
2 4 2
4 6 2
3 6 3
1 3
6 6
1 2 1
2 3 1
5 2 2
2 4 2
4 6 2
3 6 3
1 6
6 6
1 2 1
2 3 1
5 2 2
2 4 2
4 6 2
3 6 3
6 6
4 3
1 2 1
1 3 1
4 1 1
2 3
6 7
1 2 43
1 3 34
4 6 43
6 3 43
2 3 43
5 3 43
4 5 43
1 6

1
2
0
1
1

3
7 9
2 4 1
3 6 1
2 3 5
1 7 1
4 7 1
2 5 4
5 4 4
3 4 1
3 7 1
5 3
6 5
6 5 83691
4 1 83691
5 4 83691
3 2 83691
4 3 83691
5 1
6 7
6 1 83691
6 2 83691
2 5 83691
5 6 83691
2 3 83691
5 4 83574
3 5 83691
1 4

2
1
2

提示

第一个示例的地铁图如图所示。

在第一个测试用例中，从顶点 $1$ 到顶点 $3$ ，可以沿着路径行进 $1 \rightarrow 2 \rightarrow 3$ , 仅使用绿线。

在第二个测试用例中，从顶点 $1$ 到顶点 $6$ , 你可以沿着这条路旅行 $1 \rightarrow 2 \rightarrow 3 \rightarrow 6$ , 使用绿线和蓝线。

在第三个测试用例中，不需要从顶点 $6$ 移动到同一个顶点，所以行数为 $0$ 。

在第四个测试用例中，图的所有边都属于一条线，所以答案是 $1$ 。