题目背景

由于没有 SPJ 的缘故，可以进入洛谷提交。

点我跳转至洛谷

做完后记得选择这个选择题。 {{ select(1) }}

• 提交并且通过了

题目描述

给你一个由 $n$ 个顶点和 $m$ 条边组成的图形。无法保证所给图形是连通的。有些边已经定向，您无法改变其方向。其他边是无向的，您必须为所有这些边选择某个方向。

您必须以这样一种方式引导无定向边，即生成的图是有定向且无循环的（即所有边都是有向且无环的图）。请注意，您必须引导所有的无向边。

您必须回答 $t$ 个独立的测试案例。

输入格式

输入的第一行包含一个整数 $t$ ( $1 \le t \le 2 \cdot 10^4$ )--测试用例数。然后是 $t$ 个测试用例。

测试用例的第一行包含两个整数 $n$ 和 $m$ （ $2 \le n \le 2 \cdot 10^5$ , $1 \le m \le min(2 \cdot 10^5, \frac{n(n-1)}{2})$ ），分别是图中的顶点数和边数。

接下来的 $m$ 行描述图形的边。 $i$ /th边用三个整数 $t_i$ 、 $x_i$ 和 $y_i$ （ $t_i \in [0; 1]$ 、 $1 \le x_i, y_i \le n$ ）来描述--边的类型（如果是无向边，则为 $t_i = 0$ ；如果是有向边，则为 $t_i = 1$ ）和该边连接的顶点（无向边连接顶点 $x_i$ 和 $y_i$ ，有向边从顶点 $x_i$ 到顶点 $y_i$ ）。保证图中不包含自循环（即从顶点到自身的边）和多条边（即每对边（ $x_i, y_i$ ）不存在其他对边（ $x_i, y_i$ ）或（ $y_i, x_i$ ））。

保证总和 $n$ 和总和 $m$ 都不超过 $2 \cdot 10^5$ ( $\sum n \le 2 \cdot 10^5$ ; $\sum m \le 2 \cdot 10^5$ )。

输出格式

对于每个测试用例，如果不可能将无向边引导成有向无环图，则打印答案 NO，否则在第一行打印 YES，然后打印 $m$ 行，描述所生成的有向无环图的边（顺序不限）。请注意，您不能改变已定向边的方向。如果有多个答案，可以打印任意答案。

4
3 1
0 1 3
5 5
0 2 1
1 1 5
1 5 4
0 5 2
1 3 5
4 5
1 1 2
0 4 3
1 3 1
0 2 3
1 2 4
4 5
1 4 1
1 1 3
0 1 2
1 2 4
1 3 2

YES
3 1
YES
2 1
1 5
5 4
2 5
3 5
YES
1 2
3 4
3 1
3 2
2 4
NO

提示

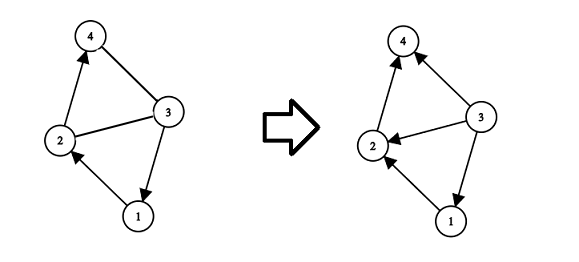
解释示例中的第二个测试用例：

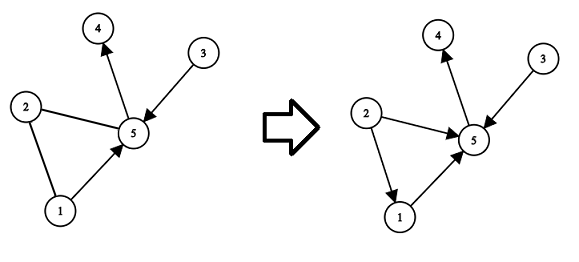
示例中第三个测试用例的解释：