#2146. CF1294F - Three Paths on a Tree
CF1294F - Three Paths on a Tree
题目背景
- 做完后记得选择这个选择题。 {{ select(1) }}
- 提交并且通过了
- 还没有提交,或者提交了
WA了。
题目描述
给定一棵含 个结点的无权树,试找出三个结点 、、
$$\operatorname{dis}(\{u,v\text{ 间的路径}\}\cup\{v,w\text{ 间的路径}\}\cup\{w,u\text{ 间的路径}\}) $$即路径的并集长度最大。
你需要输出两行:
第一行为 $\max\operatorname{dis}(\{u,v\text{ 间的路径}\}\cup\{v,w\text{ 间的路径}\}\cup\{w,u\text{ 间的路径}\})$
第二行三个整数,即 、、,如有多种答案,输出一种即可。
输入格式
第一行包含一个整数 ( ) - 树的顶点数。
接下来的 行以 ( , , )的形式描述了树的边。可以保证所给图形是一棵树。
输出格式
第一行打印一个整数 即三个点简单路径并集的最大值。
在第二行中打印三个整数 ,即 和 。
如果有多个答案,可以任意打印。
8
1 2
2 3
3 4
4 5
4 6
3 7
3 8
5
1 8 6
提示
与第一个示例相对应的图片(以及另一个正确答案):
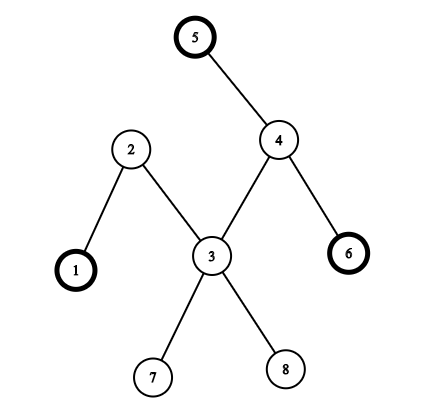
如果选择顶点 ,那么 和 之间的路径由边 组成, 和 之间的路径由边 组成, 和 之间的路径由边 组成。这些路径的合集为 ,因此答案为 。可以证明没有更好的答案。
