初赛其余习题分类练习
进制转换
十进制整数转其余进制
数位拆分,余数倒着排列。
- 例如 进制的 转 进制过程如下
13 / 2 = 6 …… 16 / 2 = 3 …… 03 / 2 = 1 …… 11 / 2 = 0 …… 1
所以 进制的 转 进制后为
- 转八进制和十六进制等其余进制将除数改为对应的数字即可。
其余进制整数转十进制
按位展开
- 例如 进制的 $1234=1\times 10^3+2\times 10^2+3\times 10^1+4\times 10^0$
那么 进制的 $(1101)_2=1\times 2^3+1\times 2^2+0\times 2^1+1\times 2^0=(13)_{10}$
- 其余进制转十进制以此类推。
小数之间的转换
- 十进制小数转二进制
整数和小数分开处理
- 整数转二进制就是数位拆分
- 小数采取乘 取整法,将得到的整数部分 正序排列
例如 转二进制。
整数部分 的二进制是
小数部分的 采取如下步骤
- ,整数部分为
- ,整数部分为 ,小数部分为 ,转化结束。
因此 转二进制就是 。
综合整数和小数部分一起,可以得到 的二进制为
- 二进制小数转十进制
- 在二进制整数中,最后一位代表 ,那么越过小数以后开始是 的几次方?
答:: 次方。
因此 转十进制就是
$$\begin{aligned} (1010.01)_2&=1\times 2^3+0\times 2^2+1\times 2^1+0\times 2^0+0\times 2^{-1}+1\times 2^{-2}\\ &=8+0+2+0+0+0.25\\ &=10.25 \end{aligned} $$其余进制以此类推。
位运算
原码,反码,补码。
原码,反码,补码是有符号数的表示方法。
计算机都是以二进制补码形式存储数,分为有符号数和无符号数;有符号位就是二进制最高位表示数字的正负。 代表正, 代表负。
int 类型的变量由于是 字节,因此一共有 个二进制位,而最高位是符号位,因此 int 类型范围可以表示的最大正整数为
$$\textcolor{red}01111111\ 11111111\ 11111111\ 11111111=2^{30}+2^{29}+\cdots+2^0=2^{31}-1 $$原码
原码将一个整数表示成符号位和它的二进制串。符号位上, 表示正数, 表示负数。
即用第一位表示符号, 其余位表示值。比如如果是 位二进制:
- 的原码为 $\textcolor{red}00000000\ 0000000\ 00000000 \ 00000001$
- 的原码为 $\textcolor{red}10000000\ 0000000\ 00000000 \ 00000001$
因此一个整数的原码就是它的二进制表示方法,同时结合最高位的符号位。
反码
正数的反码还是原码,不做任何改变。
负数的反码是除了符号位不变以外,其余位由 变 , 变 。
- 的反码为 $\textcolor{red}00000000\ 0000000\ 00000000 \ 00000001$
- 的反码为 $\textcolor{red}11111111\ 11111111\ 11111111 \ 11111110$
补码
正数的补码还是原码,不做任何改变。
负数的补码是在其反码的基础上加 得来的。
- 的补码为 $\textcolor{red}00000000\ 0000000\ 00000000 \ 00000001$
- 的补码为 $\textcolor{red}11111111\ 11111111\ 11111111 \ 11111111$
位运算简介
由于位运算是操作补码的运算,因此请务必熟练掌握原,反,补码的运算,这也是信奥赛初赛中热衷的考察点之一。
大规则:都转成二进制补码,算完了也是补码,真实值通过原码求得。
非负整数原码,反码,补码都不变。(符号位为 )
负整数求出原码后,设置符号位为 1。反码是在原码的基础上符号为不变,其他位0变1,1变0。补码由反码加 1 得到。
位运算优先级:~ , << >>, &, ^, |
| 运算符 | 含义 | 举例 | 备注 |
|---|---|---|---|
& |
按位与 | 13&12 |
都为 ,与下来才是 。否则为 |
| |
按位或 | 13 | 12 |
至少有一个 ,或下来就是 。否则为 |
^ |
按位异或 | 13 ^ 12 |
不同就为 。否则为 |
<< |
左移 | 13 << 2 |
整体向左偏移。左移多少位就是乘以 的多少次方 |
>> |
右移 | 13 >> 2 |
整体向右偏移。右移多少位就是除以 的多少次方并取整。 |
~ |
取反 | ~13 |
转成补码连同符号位在内全部 变 , 变 。 |
其余杂项
- 是数学符号,即逻辑或。 是逻辑与。 是非的意思。
优先级 ,也就是先算非,再算逻辑与,再算逻辑或。
- 字节和空间大小转换。


数据结构
栈
介绍
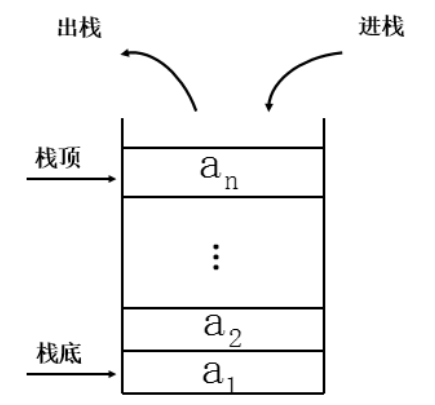
栈是 OI 中常用的一种线性数据结构,它的特点就是先进后出。如下图所示
初赛的考察点
- 熟悉栈的原理和代码
- 表达式求值的应用
- 了解和栈有关的算法原理和代码
栈的实现
- 数组模拟栈
- STL 里的
stack
数组模拟栈
由于我们需要获取栈顶元素是谁,以及能够知道数组里存放了几个元素,我们可以使用一个名为 top 的变量指向栈顶元素的下标,初始化 top = 0 意为栈内没有元素。
- 加入元素:加入一个元素,我们的做法是让 top 变量向右移动一位,然后对当前位置的元素赋值,通常写成
stk[++top] = x; - 弹出栈顶:弹出栈顶的实现方式非常简单,执行
top -= 1;即可。当然我们可以先判断一下 top 是否大于 若等于 说明栈内无元素则不执行。 - 输出栈顶元素:先判断 top 是否大于 若满足则输出
stk[top]即可。 - 栈的大小:输出 top 的值即可。
STL 里的 stack
格式:stack<元素类型> 变量名,例如 stack<int> stk;
- 加入元素:
stk.push(x) - 判断栈是否为空:
cout << stk.empty();为空输出1否则为0。 - 弹出栈顶:
if (!stk.empty()) stk.pop() - 输出栈顶元素:
if (!stk.empty()) cout << stk.top(); - 栈的大小:
cout << stk.size()即可。
判断入栈序列是否合法
该类问题通常为给定入栈序列,判断出栈序列是否合法。解决办法即用栈模拟每个选项,找到不合法的选项即可。
例如入栈序列为 a b c d e,以下哪个选项为不合法的出栈序列?
a b c d ee d c b ab a c d ec d a e b
模拟发现第四个选项错误,因为 还在 头顶呆着, 不可能先于 离开栈。
表达式求值
表达式求值要解决的问题一般是输入一个字符串表示的表达式,要求输出它的值。
例如输入一个字符串 1 + 2 * 3 人眼是很容易能够看出答案的,那么计算机是如何计算的呢?
前后缀表达式
逆波兰表达式(后缀表达式)是书写数学表达式的一种形式,其中运算符位于其操作数之后。例如,以下表达式:
可以用逆波兰表达式书写:
后缀表达式的计算方法
- 从左往右扫描字符串,遇到数字字符就入栈。
- 遇到运算符,取出栈顶两个元素,将第一个取出的元素记为 ,第二个取出的元素记为 ,如若当前运算符为 ,则计算 的结果,然后将该结果重新入栈。
- 操作完以后栈内最后剩的值就是整个表达式的结果。
例如 3 4 + 5 - 的计算过程如下
- 入栈, 入栈。
- 遇到
+,取出 ,计算 然后将 入栈 - 遇到 入栈
- 遇到
-,计算7 - 5的结果入栈
最后栈里只剩一个 即为该后缀表达式的结果。
注意事项
- 务必是后取出的 在运算符左,先取出的 在运算符右,原因是例如 的后缀表达式是 。我们是先把 入栈,再把 入栈,所以先取的是 后取的是 ,我们应当计算 而不是 。
- 在表达式合法的前提下,最终栈内必然留下一个数字是最终结果,因此不必考虑其他特殊情况,例如每次从栈里取走两个元素不必担心栈内没有两个元素的情况,若不够 个元素说明表达式是错误的。
- 后缀的好处在于没有括号,因为运算符都在数字后面,且更利于计算。
如果题目不需要我们计算真实的结果,而需要我们转中缀表达式,我们就不要把结果真的算出来,直接将整个式子入栈即可,判断何时需要括号即可。
例如 3 4 + 5 - 的计算过程如下
- 入栈, 入栈。
- 遇到
+,取出 ,计算 然后将3 + 4入栈 - 遇到 入栈
- 遇到
-,取出栈顶的两个,将3 + 4 - 5入栈,这也就是原来的中缀表达式。
前缀表达式
前缀表达式的求解类似于后缀,需要注意以下几点:
- 由于前缀是运算符在前,数字在后,所以需要从右往左倒着遍历字符串。
- 遇到运算符以后取出栈顶元素记为 ,再取出一个栈顶元素记为 ,设运算符为 ,将 的结果重新入栈即可。
中缀转后缀
- 首先根据运算符的优先级,重新加上括号
- 去括号的时候,从外向内去,每次就把运算符写到自己所在这一层的括号后即可。
例如 a * (b + c) * d 转后缀的步骤如下:
- 加括号可得
( (a * (b + c)) * d) - 去掉最外层括号,将
*移到括号右,可得(a * (b + c)) d * - 去掉最外层括号,将
*移到括号右,可得a (b + c) * d * - 去掉最外层括号,将
+移到括号右,可得a b c + * d *
括号表达式判定
形如给你一个括号表达式,你要判断括号是否合法?
- 从左往右扫描括号字符串
- 遇到左括号入栈
- 遇到右括号,若栈不为空,说明栈顶的左括号就是和当前右括号匹配成一对,匹配成功就出栈。
否则说明这个右括号没有左括号匹配,括号不合法。
队列
介绍
队列(queue)是一种具有「先进入队列的元素一定先出队列」性质的表。由于该性质,队列通常也被称为先进先出(first in first out)表,简称 FIFO 表。
实现方式
- 数组模拟队列
- STL 的 queue
数组模拟队列
首先根据数据范围定义一个数组,以最基础的数据类型都为 int 为例,例如 int q[N];
使用两个变量标记队列的头部和尾部,通常使用 int h = 1, t = 0; 设置为 和 表明当 说明队列里还没有元素。
- 插入元素:
q[++t] = x;加入元素移动队尾这个变量。 - 删除队头元素:
h++; - 访问队首:
cout << q[h]; - 访问队尾:
cout << q[t]; - 清空队列:
h = 1, t = 0; - 队列元素个数:
cout << t - h + 1;
STL 的 queue
使用方法为 queue<元素类型> 队列名字
- 插入元素:
q.push(x)。元素加入到队尾。 - 删除队头元素:
q.pop();注意保证队列不为空在使用。 - 访问队首:
cout << q.front();注意保证队列不为空在使用。 - 访问队尾:
cout << q.back();注意保证队列不为空在使用。 - 清空队列:使用
while循环遍历队列,进行pop()操作。例如:while (q.size()) q.pop(); - 队列元素个数:
cout << q.size(); - 队列是否为空:
cout << q.empty();为空返回true否则返回false
初赛的考察点
- 模拟队列的操作做选择题。
- 队列是和广度优先搜索算法搭配使用。
链表
介绍
链表是一种用于存储数据的数据结构,通过如链条一般的指针来连接元素。它的特点是插入与删除数据十分方便,但寻找与读取数据的表现欠佳。
和数组的区别
- 链表因其链状的结构,能方便地删除、插入数据,操作次数是 。但也因为这样,寻找、读取数据的效率不如数组高,在随机访问数据中的操作次数是 。
- 数组可以方便地寻找并读取数据,在随机访问中操作次数是 。但删除、插入的操作次数是 次。
单向链表
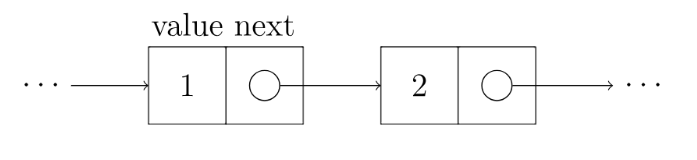
单向链表中包含数据域和指针域,其中数据域用于存放数据,指针域用来连接当前结点和下一节点。
单向链表的插入
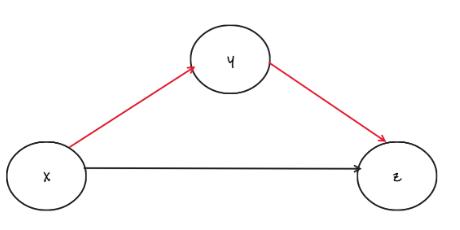
原本是黑色链接,我们要改为 条红色链接}xyyz$,按照如下代码即可实现。
y->next = x->next
x->next = y
二者顺序不能调换。
单向链表的删除
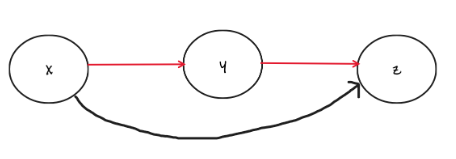
如图所示删去 就要让 直接连向 , 原本属于 的下一个,即 的下一个的下一个。
x->next = x->next->next( 的右边直接指向 达到删除 的效果)
双向链表
双向链表中同样有数据域和指针域。不同之处在于,指针域有左右(或上一个、下一个)之分,用来连接上一个结点、当前结点、下一个结点。
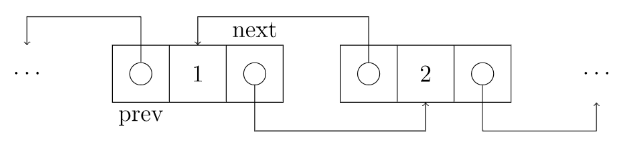
双向链表的删除

如果要删除 和 之间的 我们就要让原本红色的连接变为黑色连接。即让 的右边指向 , 的左边指向 。可以通过以下代码实现:
y->next->prev = y->prev;y->prev->next = y->next;
双向链表的插入

当我们给 和 之间插入 的时候,我们需要建立四条连接,如图 所示,可通过如下代码完成:
y->next = x->next;(第 条边)y->next->prev = y;(第 条边)y->prev = x;(第 条边)x->next = y;
初赛考察点
- 考察链表的基本概念和插入删除复杂度。
- 考察插入和删除的代码理解
- 头插法和尾插法(在链表头部或尾部插入元素)
树和图
- 图的存储和入度出度,有向图无向图,简单图,连通图等概念。
- 图的 DFS, BFS 的过程可以理解。
- 拓扑排序
- 二叉树的基本概念,完全二叉树和满二叉树。
- 二叉树的前中后序遍历,可以根据中序加前序推第三个序列,
- 霍夫曼编码的构造方法和判断。
- 状态
- 已结束
- 规则
- IOI
- 题目
- 12
- 开始于
- 2024-9-5 15:15
- 结束于
- 2024-9-22 7:15
- 持续时间
- 400 小时
- 主持人
- 参赛人数
- 40
